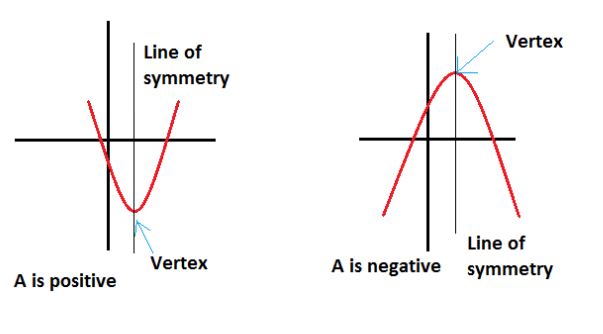
A quadratic can be generally expressed as ax²+bx+c. The vertex of a quadratic is the lowest point (a is positive) or the highest point (a is negative). The line of symmetry of a quadratic can be expressed as x=n, where n equals the x coordinate of the vertex.
To calculate where the vertex is, we need to complete the square, which we'll come on to later.
You should know that the general solutions of quadratic equations in the form ax²+bx+c = 0 is x = (-b±√(b²-4ac))⁄2a. The discriminant is in this, and it is b²-4ac. This tells us if the equation has any real roots, and if it does, how many. It can be either positive, zero or negative. If it is positive, then the equation has 2 real roots as the square root of it is real and is either taken away or added. If it is zero, then the equation has one real root as the square root of b²-4ac is 0 and adding and taking away 0 gives the same answer. If b²-4ac is negative then it has no real roots as the square root of a negative number is imaginary (i.e- unreal) and so any solutions will not take a real value.
There are 3 ways that they can be solved. You could be asked about any of them!
If the quadratic you are asked to solve can be easily factorised and you are allowed to do so, then do so as it is the quickest and easiest way. For example, if you are given the quadratic 2x²+x-6 = 0 then it can be factorised to (2x-3)(x+2) = 0 , so then 2x-3 = 0 so x = 1.5 and x+2 = 0 so x also = -2, therefore x = 1.5 or x = -2. This is also how the x intercept(s) of a quadratic is/are figured out.
As stated earlier, completing the square is used to figure out the vertex of the graph and also its solutions. If we have the quadratic x²-6x+2, it can be rewritten as (x-3)²-9+2 = (x-3)²-7. How is this used to find out the solutions? If x²-6x+2 = 0, then (x-3)²-7 = 0 so (x-3)² = 7, so squaring both sides gives x-3 = √7, so x = √7+3. This gives two solutions, as √7 can be either positive or negative. This process can be used to find its vertex as if we go back to (x-3)²-7 = 0, this is a transformation of an x² graph. This will be covered in more depth in the 'Graphing and Manipulating Equations' section, but for this graph it's a translation of 3 right and 7 down, hence the vertex is at (3,-7).
This can be also done with more complex quadratics, for example 2x²+4x-5. Firstly, it can be rewritten as 2(x²+2x)-5 = 2((x+1)²-1)-5 =2(x+1)²-2-5 = 2(x+1)²-7. This can also be solved to find x, so 2(x+1)² = 7 => (x+1)² = 3.5 => x+1 = √3.5 => x = √3.5 -1. The vertex can also be found using the previous method, as the 2 doesnt affect the vertex.
This is the simplest method to use, as values have to be substituted into (-b±√(b²-4ac))⁄2a.